LACCTiC

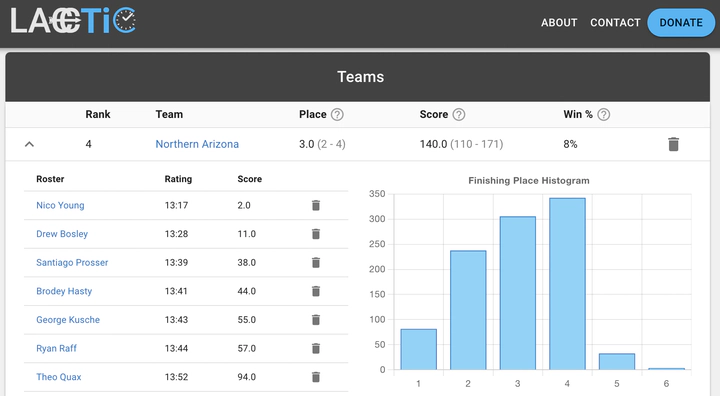
LACCTiC.com is a website that I developed in 2021 to convert cross country performances from varying course difficulties to their track 5k equivalents. The results are used to provide sophisticated rankings and race simulations. The aglorithm has evoled over time and has many small tweaks, but I will provide a short summary of the ideas here.

The main idea behind LACCTiC is to look at how finish times change across different courses. This won’t be informative for a single runner, who may have had a good and bad race. However, the average across many runners should give an idea of the course’s relative difficulty since the same number of people will have had good races and bad races.

Consider $n$ runners who run $m$ races. Notice that if we had runner fitness estimates, then we could use those estimates to estimate course adjustments. Similarly, if we had course adjustments, we could use those course adjustments to estimate runner fitness. We have neither, but we can start with a guess on some runners’ fitnesses using their 5k PRs, then switch back and forth finding course adjustments and estimating fitnesses until we converge. This is sometimes called an “expectation maximization” approach. Now, lets go into the details…

First, suppose you knew everyone’s average 5k finesses, e.g., $f_1,f_2,\dots ,f_n$. If you did, then you could go to the $j$th race and compare everyone’s times $t_1^{(j)},t_2^{(j)},\dots ,t_n^{(j)}$ (here $t_i^{(j)}$ is runner $i$’s time for race $j$). We can now find some ${\alpha }_j$ that describes the ratio between times in race $j$ and people’s general fitnesses. That is, we want ${\alpha }_j{t}_1,\alpha t_2,\dots ,{\alpha }_j{t}_n$ to be close to $f_1,f_2,\dots ,f_n$. Let’s use an average, so

$${\alpha }_j=\frac{\sum _i{f}_i}{\sum _i{t}_i}.$$

We will call ${\alpha }_j$ the “adjustment” for the course because multiplying a runner’s time on course $j$ times ${\alpha }_j$ approximately gives us the 5k equivalent. Slower courses will have slower times, meaning ${\alpha }_j$ will be smaller.

Now, suppose we knew all of the course adjustments (${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_m$). We could use all of these course adjustments to give every runner a list of adjusted times, e.g., runner $i$ would now have adjusted times ${\alpha }_1{t}_i^{(1)},{\alpha }_2{t}_i^{(2)},\dots ,{\alpha }_m{t}_i^{(m)}$. We can average these times to get an estimate of each runner’s fitness:

$$f_i=\sum _{j=1}^m{t}_i^{(j)}/m.$$

We alternate between these two computations. Calculating the ${\alpha }_j$s refines estimates of course adjustments, which can then be used to get better estimates for runner fitnesses ($f_i$s), which can then be used to further refine course adjustments, and so on.

Once we converge on solutions, we need to make sure that adjusted cross country season PRs line up with track PRs (we only used track PRs as an initial guess). To do this, we shift everyone’s adjustments and scores so that (on average) people’s best converted times equate to their track PRs. Of course, some people will be better than track and some will be worse.

A detail I’ve left out here is that not all runners run every course! If you go back through the equations, you should find that none of them require full participation from every runner. However, in order to get good results, we need to not have any “islands,” such as conferences that only race themselves and never have any comparison to the outside world.