Source Identification for Mixtures of Product Distributions

Abstract

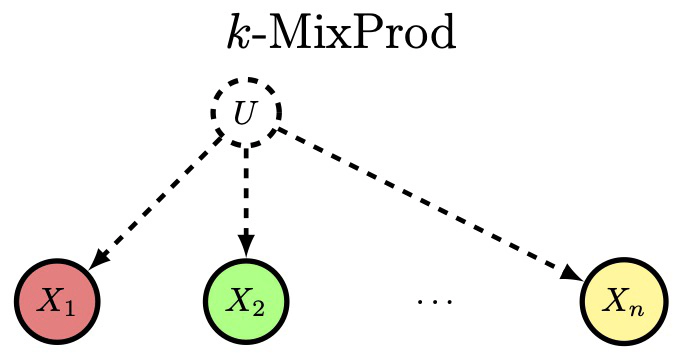
We give an algorithm for source identification of a mixture of $k$ product distributions on $n$ bits. This is a fundamental problem in machine learning with many applications. Our algorithm identifies the source parameters of an identifiable mixture, given, as input, approximate values of multilinear moments (derived, for instance, from a sufficiently large sample), using $2\mathcal{O}(k^2)n\mathcal{O}(k)$ arithmetic operations. Our result is the first explicit bound on the computational complexity of source identification of such mixtures. The running time improves previous results by Feldman, O’Donnell, and Servedio (FOCS 2005) and Chen and Moitra (STOC 2019) that guaranteed only learning the mixture (without parametric identification of the source). Our analysis gives a quantitative version of a qualitative characterization of identifiable sources that is due to Tahmasebi, Motahari, and Maddah-Ali (ISIT 2018).

Bijan Mazaheri

My interests include mixture models, high level data fusion, and stability to distribution shift - usually through the lense of causality.