Identification of Mixtures of Discrete Product Distributions in Near-Optimal Sample and Time Complexity

Abstract

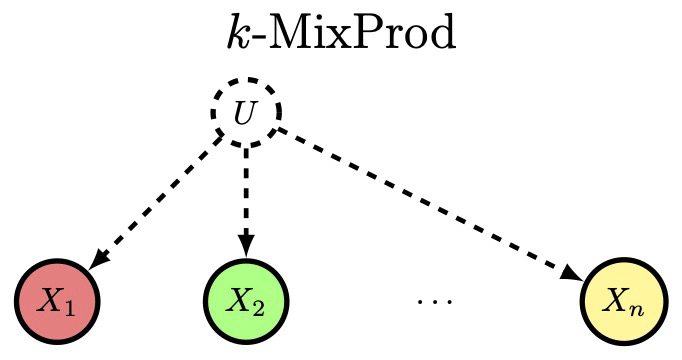
We consider the problem of identifying, from statistics, a distribution of discrete random variables $X_1,\dots ,X_n$ that is a mixture of $k$ product distributions. The best previous sample complexity for $n\in O(k)$ was $(1/\zeta {)}^{O(k^2\log k)}$ (under a mild separation assumption parameterized by $\zeta$). The best known lower bound was $\exp (\mathrm{\Omega }(k))$. It is known that $n\ge 2k-1$ is necessary and sufficient for identification. We show, for any $n\ge 2k-1$, how to achieve sample complexity and run-time complexity $(1/\zeta {)}^{O(k)}$. We also extend the known lower bound of $e^{\mathrm{\Omega }(k)}$ to match our upper bound across a broad range of $\zeta$. Our results are obtained by combining (a) a classic method for robust tensor decomposition, (b) a novel way of bounding the condition number of key matrices called Hadamard extensions, by studying their action only on flattened rank-1 tensors.

Bijan Mazaheri

My interests include mixture models, high level data fusion, and stability to distribution shift - usually through the lense of causality.