Synthetic Potential Outcomes and Causal Mixture Identifiability

Abstract

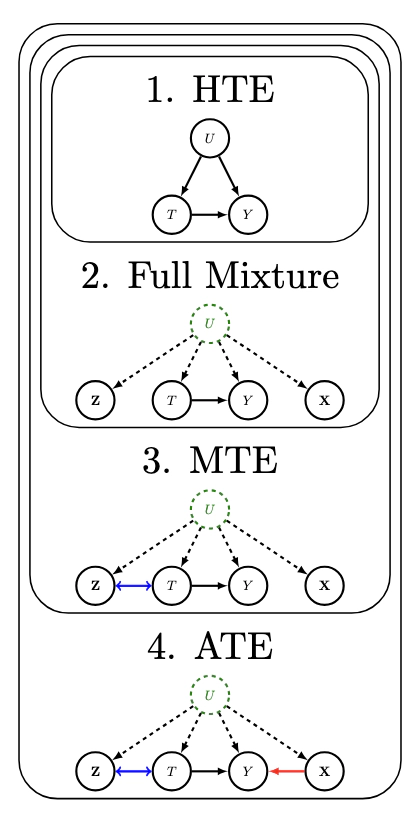
Heterogeneous data from multiple populations, sub-groups, or sources can be represented as a “mixture model” with a single latent class influencing all of the observed covariates. Heterogeneity can be resolved at different levels by grouping populations according to different notions of similarity. This paper proposes grouping with respect to the causal response of an intervention or perturbation on the system. This is distinct from previous notions, such as grouping by similar covariate values (e.g., clustering) or similar correlations between covariates (e.g., Gaussian mixture models). To solve the problem, we “synthetically sample” from a counterfactual distribution using higher-order multi-linear moments of the observable data. To understand how these ``causal mixtures’’ fit in with more classical notions, we develop a hierarchy of mixture identifiability.

Bijan Mazaheri

My interests include mixture models, high level data fusion, and stability to distribution shift - usually through the lense of causality.