Distribution Shift and Conterfactual Features
The principle assumption when building any (not necessarily causal) prediction model is access to relevant data for the task at hand. When predicting label $Y$ from inputs $\mathbf{X}$, this assumption reads that the data is drawn from a (training) probability distribution $\mathbf{X}, Y$ that is identical to the distribution that will generate its use-cases (target distribution).
Unfortunately, the dynamic nature of real-world systems makes obtaining perfectly relevant data difficult. Data gathering mechanisms can introduce sampling bias, yielding distorted training data. Even in the absence of sampling biases, populations, environments, and interventions give rise to distribution shifts in their own right.
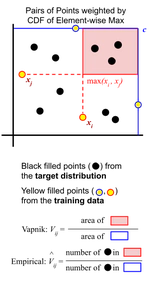
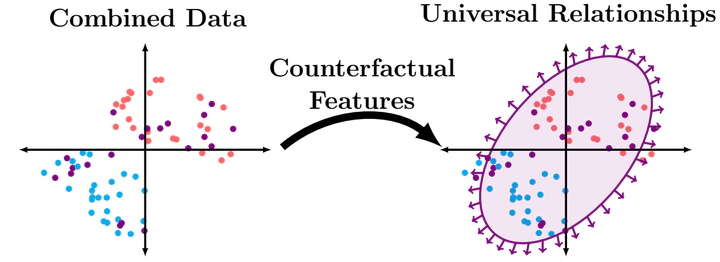
Fusing data sources also fuses the support on which our models are expected to perform well, but we are still limited to the situations we have seen. If we want generalization outside of our gathered data, we need to build models that are invariant to the mechanisms that can modify the distribution. Physicists have successfully determined “universal” laws using extremely precise measurements of simple systems. The setting becomes challenging when our data is limited to proxies of the underlying components of complex systems, as is often the case with medical data.
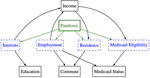
One surprising fact is that augmenting models with “counterfactual features” (motivated by the causal-structure) can improve model robustness to distrbution shift. As an example, we have looked at income prediction on US census data using education level, commute time, and medicaid status – all three of which were shifted by the pandemic. Building a model on “education” and the answer to the question “What education level would we expect, if the individual were high income, based on the individual’s commute time and medicaid status?” is more stable than the naive choice of all three features. The answer to the counterfactual question is easily obtained from training a model to predict education using commute time on only high-income data.