Abstract
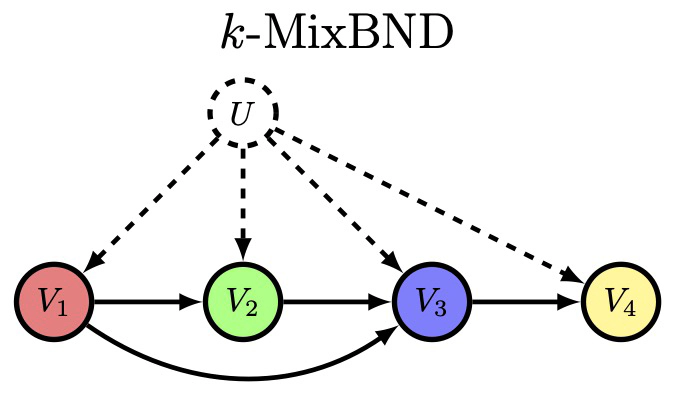
A Bayesian Network is a directed acyclic graph (DAG) on a set of $n$ random variables (the vertices); a Bayesian Network Distribution (BND) is a probability distribution on the random variables that is Markovian on the graph. A finite $k$-mixture of such models is graphically represented by a larger graph which has an additional “hidden” (or “latent”) random variable $U$, ranging in ${1,\ldots,k}$, and a directed edge from $U$ to every other vertex. Models of this type are fundamental to causal inference, where $U$ models an unobserved confounding effect of multiple populations, obscuring the causal relationships in the observable DAG. By solving the mixture problem and recovering the joint probability distribution on $U$, traditionally unidentifiable causal relationships become identifiable. Using a reduction to the more well-studied “product” case on empty graphs, we give the first algorithm to learn mixtures of non-empty DAGs.
Bijan Mazaheri
Postdoctoral Scholar
My interests include mixture models, high level data fusion, and stability to distribution shift - usually through the lense of causality.